This article came out of a question I asked myself yesterday.
“Is there a year in which no month begins on Monday?”
At first glance, yes.
The year can begin on any day of the week, and the months also begin on different days of the week each time. There are many options, most likely there will be more than one such year. That's what I thought the first minute after I asked the question. This should have been proven. Go through all the years, for example. A simple and fast way, but not interesting. Proving it mathematically was a much more tempting idea, but I had absolutely no idea how to approach it. So I just started writing out the duration of each month on paper. Here it is worth mentioning that we will further discuss the Gregorian calendar, according to which we have been living since 1918. However, some of the reasoning will be true for the Julian one. In fact, there is no such year. Let's figure out why.
Part 1. Months
First, let's remember how many days there are in each month:
| Jan | Feb | March | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec |
| 31 | 28 / 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Now let's see how many days in each month there are more than four weeks.
| Jan | Feb | March | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec |
| 3 | 0 / 1 | 3 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 3 |
At this point the following idea arises. If you add 7 days to the date, the day of the week will not change. Modular arithmetic works. From here it is easy to understand that if there are two more days in a month than in four weeks, then the first day of the next month will shift by two days of the week relative to the first day of the current month. And in general,
if there are (28 + N) days in a month, then the first day of the next month will shift by N days relative to the day of the week of the first day of the current month.
For example, this year January started on a Tuesday, so February started on a Friday.
Tue + 3 = Fri. How much does the day of the week shift on the first day of a certain month? To find this, you need to sum up the “excess” days over four weeks in all previous months. The table shows the shifts relative to the day of the week on the first of January. The first line is for non-leap years, the second for leap years.
| Jan | Feb | March | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec |
| 0 | 3 | 3 | 6 | 8 | 11 | 13 | 16 | 19 | 21 | 24 | 26 |
| 0 | 3 | 4 | 7 | 9 | 12 | 14 | 17 | 20 | 22 | 25 | 27 |
But this does not look very significant, and we know that a shift of seven days does not change the day of the week. Therefore, let us now write down in the table the remainders from dividing the total shifts by 7.
| Jan | Feb | March | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec |
| 0 | 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
| 0 | 3 | 4 | 0 | 2 | 5 | 0 | 3 | 6 | 1 | 4 | 6 |
Now it's a different matter! It is clearly visible how to determine the day of the week for the first day of any month if the day of the week for the first of January is known. You just need to add the shift for the month of interest. I have known the February-March-November pattern since school, but I haven’t noticed others.
We received the answer to the question at the beginning of the article.
Since for both versions of the year the table contains all shifts from 0 to 6, then in any year there is a month that begins on a specific day of the week.
But now you can ask other questions. For example, “in which years there is only one such month?” or “in which years do you have the most such months?” To do this, you need to be able to determine the day of the week on the first of January of any year.
Pregnancy by month
As soon as you become pregnant, your baby will begin to grow and from a very microscopic embryo in a few months will turn into a toddler about half a meter tall. Its growth rate is many times higher than your growth rate during pregnancy.
If you are not interested in reading about the baby’s development week by week, then below is a quick overview of the processes taking place in the child’s body month by month. Here we will not touch upon aspects relating to the expectant mother at all.
1st month of pregnancy
After conception has occurred, the multicellular zygote descends down the fallopian tube and takes hold in the uterus. This process took about a week. But even in this short period of time, the child has already become 10,000 times larger than the cells from which he “emerged.” By the end of the first month of pregnancy, the baby is already the size of a grain of rice. His brain, spinal cord and head began to develop.
2nd month of pregnancy
In the second month, the fetus consists of three “layers”. The first of them - the top one - is the ectoderm. It will form the skin, hair, nervous system, as well as the mucous membranes of the baby’s nose, ears and mouth. From the second layer - under the ectoderm - his heart, muscles, bones, blood and reproductive system will develop. The third layer "morphs" into your baby's glands, tongue, bladder and gastrointestinal tract. The baby's heart is the first to form and will begin beating by the end of the second month. Your baby at this stage will be approximately the size of a grain of corn.
3rd month of pregnancy
During the third month, the baby's nails, earlobes, arms, legs, hands, feet, and fingers and toes develop. The intestines are also already formed. But at first it all may seem a little “under-formed”. The human body will become recognizable only by the end of the month. At the end of the 3rd month, the baby will weigh about the same as a tube of lipstick. Another important “achievement” is that he is already able to empty his bladder into amniotic fluid.
4th month of pregnancy
The fourth month is usually associated with the development of the baby's genital organs. The baby can already blink and suck, and the skin becomes yellowish. The child is also able to move his pupils and look in different directions. By the end of the month, it will be comparable in size to an average banana.
5th month of pregnancy
At this stage, the baby is already able to make some movements that you will feel in the uterus. Eyebrows and eyelashes are formed. A small tuft of hair will already appear on the head. A child in the 5th month of pregnancy weighs on average 450 grams.
6th month of pregnancy
The child's body is enveloped in a white substance - vernix. It helps protect the baby from abrasions and skin cracking that can occur due to prolonged exposure to amniotic fluid. If you are expecting a girl, eggs will already begin to form in her ovaries. It turns out that you are not only expecting a daughter, but in her body everything is already prepared for your future grandchildren. By the end of the month, the baby will double his weight - he now weighs approximately 900 grams.
7th month of pregnancy
So now your child can hear you. It can respond to loud sounds as well as music. The taste buds are almost completely formed. The baby can clench his fists and grab things. By the end of the seventh month the baby will weigh about 1 kg 800 g.
8th month of pregnancy
All the main organs and systems have already been developed; the final “touches” remain. The child's pupils are already able to contract and dilate in response to light. The lungs are perhaps the last major organ that is not yet fully developed. Nevertheless, the baby has already begun to practice breathing (so far he is breathing not oxygen, but amniotic fluid). The child's weight is about 2.2 kg.
Part 2. Years
When I was learning to program, and this was in the 10th grade of school using PascalABC, one of the first serious tasks was to implement a procedure that printed a calendar for the year, which was passed as an argument.
We had hints on what functions needed to be implemented for this. In general, it all came down to counting the days between two dates: the reference and the current, in order to determine the day of the week on the first of January of the desired year. This approach worked, but the speed depended on how close the required year was to the reference year. This upset me, but I couldn’t come up with something better then. Now is the perfect moment to fully understand this.
Leap years in the Gregorian calendar are assigned as follows:
- A year whose number is a multiple of 400 is a leap year.
- other years, the number of which is a multiple of 100, are non-leap years
- the rest of the years, the number of which is a multiple of 4, are leap years
- other years are non-leap years
From this description it is clear that the leap cycle has a period of 400 years.
But it is not clear whether such four-hundred-year cycles will begin on the same day of the week. Note that the first of January shifts by one or two days of the week from year to year, and we write
a little code.
bool is_leap_year(int year) { if ((year % 400) == 0) return true;
if ((year % 100) == 0) return false; if ((year % 4) == 0) return true; return false; } void first_weekdays_table() { ofstream file("weekdays.txt", ios_base::out); int weekday = 3; for (int i = 1801; i <= 3000; ++i) { file << weekday; if ((i % 100) != 0) { file << " "; } else { file << endl; } weekday += is_leap_year(i) ? 2 : 1; weekday %= 7; } file.close(); } The days of the week are displayed on the first of January of each year, from 1801 to 3000. Monday is designated as “0”, Tuesday as “1”, etc. Let’s imagine everything in the form of a table of two full four-hundred-year cycles and two halves. Centuries go horizontally, and years go vertically in these centuries. The day of the week on which this year began is written in the cells at the intersection of the century and the year. For example, the day of the week on which 1997 began is at the intersection of column "1900" and row "97". This is Wednesday. Full version of the table:
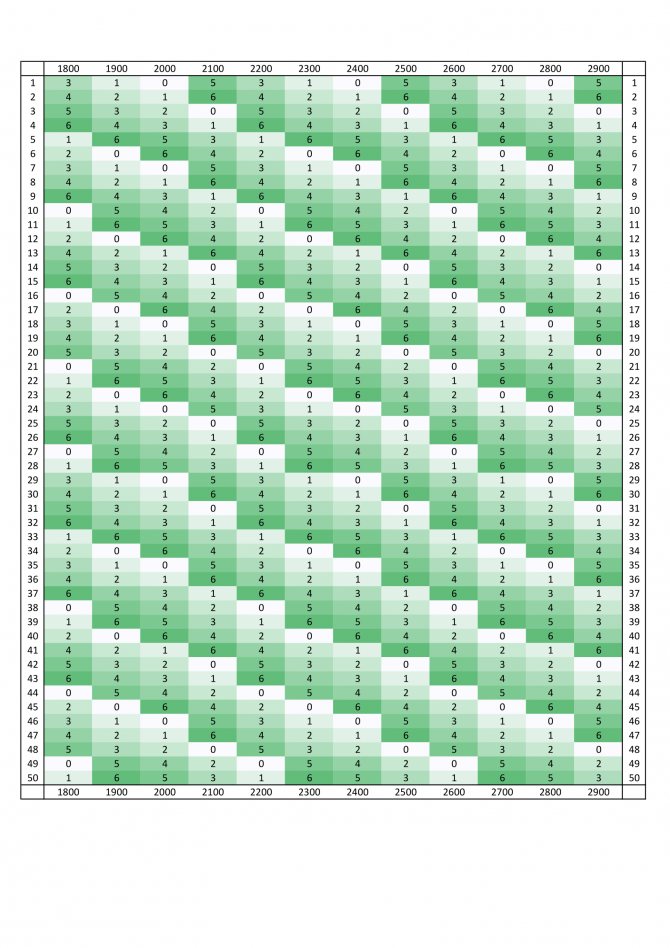
,
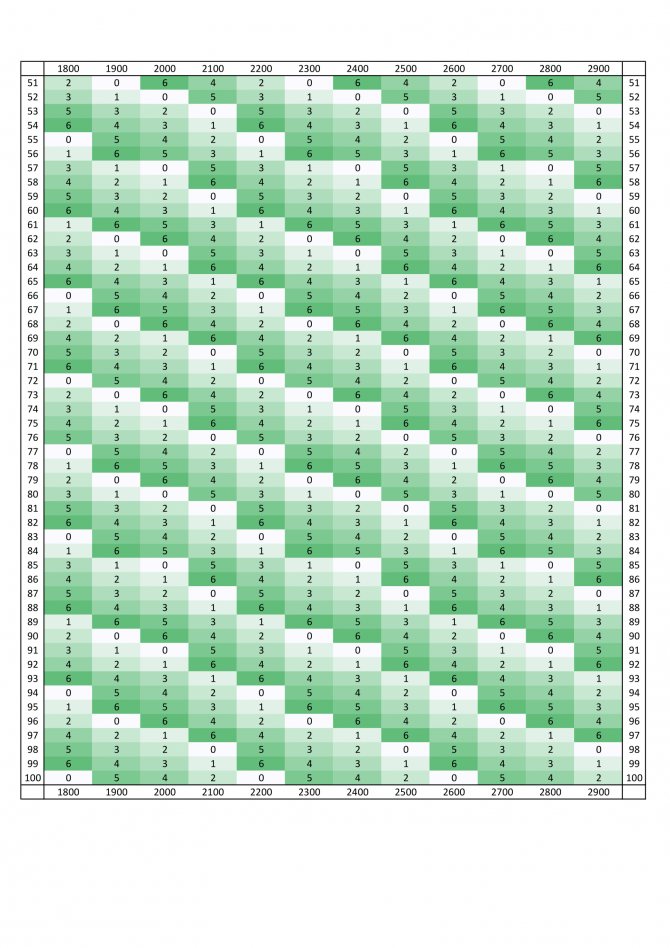
. You can immediately notice two things in the table: the four-hundred-year cycles actually begin on one day of the week (2001, 2401 and 2801; Monday), and instead of the year 2000 there is “one thousand nine hundred and one.” The latter was done on purpose, for further convenience. The first fact allows us to move on without obstacles.
In the Gregorian calendar, all four-hundred-year cycles begin on Monday.
But the most interesting thing lies in the full version of the table. It can be found that each century within the four-hundred-year cycle consists of a repeating twenty-eight year cycle:
| 0 | 1 | 2 | 3 | 5 | 6 | 0 | 1 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 6 | 0 | 1 | 2 | 4 | 5 | 6 | 0 | 2 | 3 | 4 | 5 |
The first century begins with a cycle offset equal to 0, the second with an offset of 4, the third with an offset of 8 and the fourth with an offset of 12. It is for this purpose that the table is presented in the form where the century has “hundredths” of the year and no zeros. It is worth saying that there are a total of 14 different year options. In the twenty-eight-year cycle, once for each day of the week there is the beginning of a leap year and three times the beginning of a non-leap year.
Now we can determine the day of the week for any date without using reference dates. To do this, we need to understand in which century within the four-hundred-year cycle the year is located and what number it is in this century. Using the table, we will determine the day of the week on the first of January of the year, and using the first part of the article, we will determine the day of the week on a specific date of the desired month. Instead of a thousand words
Let's write some more code.
int get_weekday(int year, int month, int day) { int weekdays[] = {0, 1, 2, 3, 5, 6, 0, 1, 3, 4, 5, 6, 1, 2, 3, 4 , 6, 0, 1, 2, 4, 5, 6, 0, 2, 3, 4, 5}; int shift_not_leap[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}; int shift_leap[] = {0, 3, 4, 0, 2, 5, 0, 3, 6, 1, 4, 6}; bool is_leap = is_leap_year(year); year -= 1; year %= 400; int century = year / 100; year %= 100; int index = (year + (4 * century)) % 28; int weekday = weekdays[index]; weekday += is_leap ? shift_leap : shift_not_leap; weekday += (day - 1); weekday %= 7; return weekday; }
Predictions for the month with the Number 7
Opportunities in this number
Lock your doors and windows, turn off your phone, and hang a “Do Not Disturb” sign on your front door. This month you will not need anyone for any purpose. What you really need to do is do some self-reflection and sort out your aspirations and hopes and label your goals and objectives.
While maintaining minimal external activity, put all your efforts into eliminating internal problems. Over the months of intense and fruitful work, you have somewhat forgotten how it all began, and (as a result) you could lose the right direction of movement. To begin with, once again voice the final goals of long-term projects, then formulate and itemize tasks for the near future, and then take an inventory of your desires (have they changed recently?). After this, make sure that there are still existing problems and try to answer the questions: “What specifically does not suit me and why have I still not been able to change anything for the better?”
The month of number seven is the time when you will be able to get the most accurate and most frank answers from yourself. The month of number seven is a real opportunity to get off the rails of inertia and meaningless vanity that does not bring concrete results. Something does not work? Stop habitually beating your mind and body against a blank wall and try to find the door. Or maybe you should go in a different direction altogether? The French have a wonderful saying: “Jump from the step you’re standing on,” in Russian this corresponds to the expression: “Don’t try to wishful thinking, be realistic.”
Before you get back into the daily struggle for a more comfortable place in the sun, try to clearly define the parameters that correspond to your concept of “comfort”. Do not follow the lead of people who demand the highest performance from you on all counts - this is physically impossible. It's better to clearly define in which area you can really achieve significant success, and direct most of your efforts there. The long-known and even hackneyed truth “If you love and understand yourself, it will help other people understand and love you” can easily become the motto of the month of number seven.
Warnings for the month 7
Firstly and (in our rough and materialistic life) most importantly: some financial problems may arise. They may have a different character, but most likely there is one reason - you have temporarily weakened control. Nothing major, but it’s better to hold your wallet tighter on public transport, avoid lending money to people known for their forgetfulness, check receipts in stores, and make purchases with a clear mind and sober memory.
Secondly, you may experience a sudden attack of absent-mindedness, so before leaving the house, double check that you have turned off the iron; Before picking up an interesting book, remove all pots and pans from the stove; When leaving the apartment, check for keys and money; When getting out of a taxi, check whether you left a cell phone or an umbrella in the car. And so on...
Characteristics of the month
Tendency to introspection, solitude, research, comparison, striving for perfection, absent-mindedness, cognition.
Switch to energy saving mode. No unnecessary bursts of activity. Strictly measure the amount of effort put into solving a particular problem. Try to reduce external activity as much as possible, otherwise your vitality may sharply decrease.
Colors of success this month: violet, purple, turquoise.
Maxim Fedorov
Part 3. Results
With just two tables, you can determine the day of the week for any date without using reference dates.
The sequence of days of the week on the first of January in the twenty-eight year cycle:
| 0 | 1 | 2 | 3 | 5 | 6 | 0 | 1 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 6 | 0 | 1 | 2 | 4 | 5 | 6 | 0 | 2 | 3 | 4 | 5 |
And a table of weekday offsets on the first day of each month for non-leap and leap years:
| Jan | Feb | March | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec |
| 0 | 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
| 0 | 3 | 4 | 0 | 2 | 5 | 0 | 3 | 6 | 1 | 4 | 6 |
While writing this article, I found two similar topics on Habré: one and two. The author of the first, using a special table, shows how to find the day of the week in your mind for dates in the 20th and 21st centuries. The table he presented contains 56 numbers. The algorithm proposed in the article uses a table of days of the week and two tables of offsets containing (28 + 2*12) = 52 numbers that need to be remembered. All source code is on GitHub.
Interesting fact: from February 1 to February 13, 1918, not a single person was born in Soviet Russia.
Ask yourself questions every Sunday morning =)
Update from 07/03/2019 (Wednesday)
If we represent the twenty-eight year cycle in table form, 0, 1, 2, 3, 5, 6, 0, 1, 3, 4, 5, 6, 1, 2, 3, 4, 6, 0, 1, 2, 4, 5, 6, 0, 2, 3, 4, 5 then it becomes clear how you can calculate the offset of the day of the week on the first of January: weekday = (index + (index / 4)) % 7;
Taking this into account, as well as the fact that offsets for months in a leap year can be calculated using offsets in a non-leap year, we will write the following function
int get_weekday_c(int year, int month, int day) { int shifts[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}; int shift = shifts; if (is_leap_year(year) and (month > 2)) { shift += 1; }; year = (year - 1) % 400; int century = year / 100; int index = ((4 * century) + (year % 100)) % 28; int weekday = (index + (index / 4)) + shift + (day - 1); return (weekday % 7); }
Thus, you can calculate the day of the week for any date, knowing only 12 numbers: the offset of the days of the week on the first day of each month.